生活中偶尔会出现一些分期，或者贷款的场景，要么没有标明利率，要么利率说的极具诱惑力，我想弄明白这个利率具体是多少。

这里会举一些常见的例子，并说明其计算方式

分期免息购买手机/电脑，每月固定时间还款，还固定金额

这种场景常出现在，京东上购买大件分期，假设电脑价值5000，24期免息

每月还款额： 5000/24=208.3333

大家都知道通货膨胀，现金贬值的概念，

问题1：

这笔钱是我在24期后才还完了5000元，这24期还完的5000元相当于我现在一次性付清的多少钱，假设目前的存款年利率为2.5%。

1/1/2023	208.33
2/1/2023	208.33
3/1/2023	208.33
4/1/2023	208.33
5/1/2023	208.33
6/1/2023	208.33
7/1/2023	208.33
8/1/2023	208.33
9/1/2023	208.33
10/1/2023	208.33
11/1/2023	208.33
12/1/2023	208.33
1/1/2024	208.33
2/1/2024	208.33
3/1/2024	208.33
4/1/2024	208.33
5/1/2024	208.33
6/1/2024	208.33
7/1/2024	208.33
8/1/2024	208.33
9/1/2024	208.33
10/1/2024	208.33
11/1/2024	208.33
12/1/2024	208.33

如上所示，我们知道还款日期为每月1号，且金额为 5000/24=208.3333

假设第i个月的还款额为Vi，其成本为Ci，存款月利率为r，有下列公式

意思即： 第i月的还款额 = 成本 + 成本在这i月内若用来投资产生的利息

我们将上述公式整理一下，得到每个月还款额和成本的相关关系

这里的，

我们想要得到 的值

整理下上述公式，得到下列式子

很容易看到，左边是个等比数列，使用高中学的等比数列求和方式，左右两边同乘

设，代入，

最后整理得到

代入，n=24，r=2.5%/12=0.00208，

解得Z=4872.11

也即如果我们通过24期免息分期借款5000，每月等额还款208.33，其时间价值相当于我们此刻使用4872.11元全额购买

所以，通过分期免息的方式，我们省下了128元（以及我们避免一次性支出大额金钱，让我们可以在手里有更多的钱来抵御其他风险）

上面是通过公式推导，逐步得出结果，实际上Excel中已经内置了PV函数，计算现金净值了

参见：PV 函数 – Microsoft 支持

问题2：如果我一次性投入5000元，年利率为2.5%，这笔钱在两年后的价值为多少

问题3：如果我按照等额本金的方式，每月存款5000/24元，年利率为2.5%，那么两年后（即24期后）会有多少钱

公式的推导方式和问题1一样，这里直接给答案是5121.64元，

同理可以用Excel中的FV公式直接算出，参见FV 函数 – Microsoft 支持

等额本息，等额本金两者的区别与误解

以房贷为例，我们假设我们需要向银行贷款300W，以LRP5Y 4.3%进行计算，按30年贷款（360月）计算

等额本金：每个月还固定额度的本金+ 上月产生的利息（上个月的剩余欠款总额*当月利率），这里的本金是每月300W/360(月) 元

等额本息：每个月还固定额度的还款额（本金+利息）， 利息为上月剩余欠款总额*当月利率

看起来似乎，两者的计算公式都差不多，那为什么通常等额本金的总还款额要少于等额本息呢？

原因在于上月的剩余欠款总额，两者是不同的。

不管哪种方式，本金的减少额 = 当月还款额 – 当月利息，且两种方式利率是相等的。

那么在还款的第一个月时，两者的利息都是相等的。

（当月的利息 = 剩余欠款总额 * 当月利率，因为剩余欠款总额相同，利率相同，所以利息相同）

而因为以等额本金的方式还款，每个月的本金减少额是 欠款总额 / 总月数

而选择等额本息的方式还款，每个月的本金还款额是

{{P}_{\text{n}}}={{P}_{1}}*{{(1+r)}^{n-1}}

{{P}_{1}}=P*\frac{r*{{(1+r)}^{n}}}{{{(1+r)}^{n}}-1}

P是借款本金，我们能看到在还款的过程中，本金占还款金额的比例在逐步提升。

下图为在Excel中计算借款300w，两种还款方式的每期还款信息

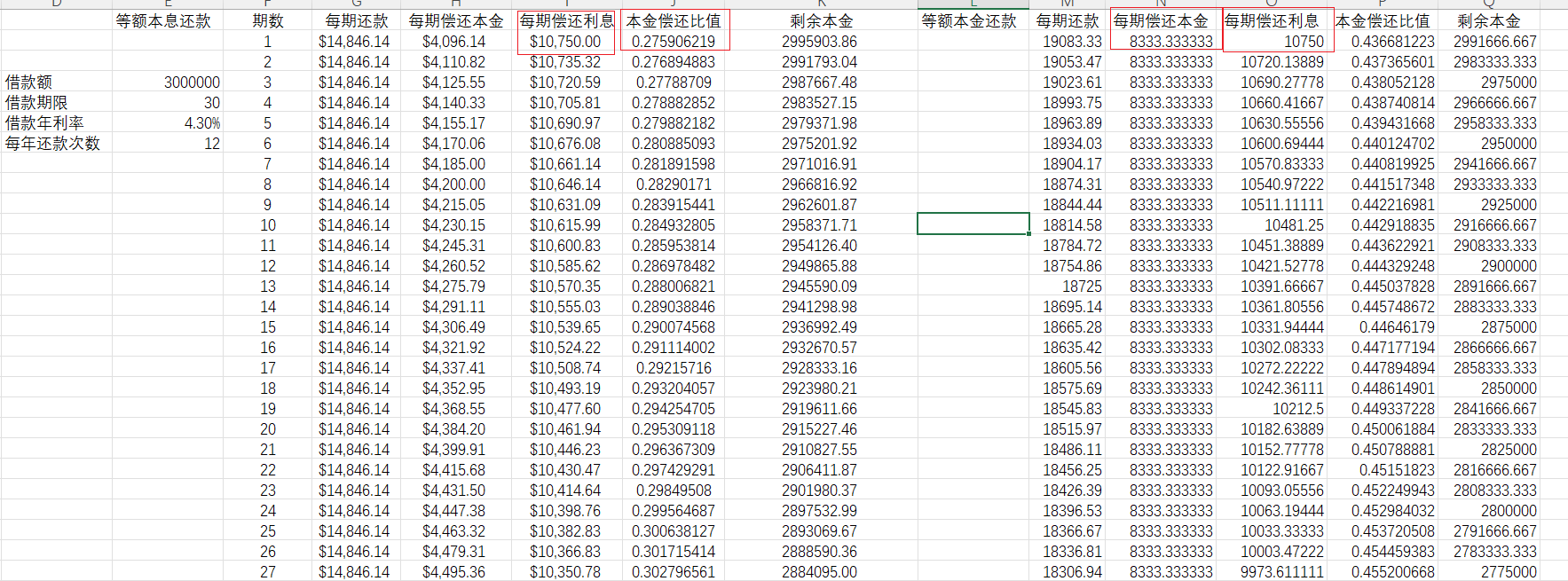
通过上图，我们能看到，在第一个月时两者的利息是一致的，但因为等额本金相对于等额本息在初始时多偿还了部分本金，从而导致后续的利息变少。

而等额本息多偿还的利息，其实也就是相当于等额本金少偿还的那部分本金在时间上所产生的本金+利息。

理论上，即使我们选择等额本息还款，也可以通过每月超额还款的方式补足本金，达到和等额本金一样的效果。

但是，这只是理论上，通常银行在签订合同的前两年都不允许超额还款，或需要支付手续费。

上图中等额本息，等额本金在Excel中如何计算可参考下列链接

等额本息：Excel：房贷还款计划，清楚明了每月的本金利息

等额本金：Excel怎么计算等额本金还款金额